무한급수

Série infinie  (영어:series infinite)

수열의 합.

 

I. 급수의 종류

	설명	우선 사항
유한급수  Série finies	항의 개수가 유한한 것	항 별로 연산 가능한지 점검
무한급수  Série infinie	항의 개수가 무한인 것	수렴여부부터 우선 점검
발산급수  Série divergente	무한수열이 극한을 가지지 않는 급수	판정법 점검 이후 시행 (발산,비교,항비,근,적분판정법등)
수렴급수   Série convergente	항의 합이 어떤 일정한값에 한없이 가까워지는 급수

 

II. 발산과 수렴

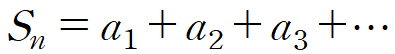
무한급수에서 발산, 수렴을 판정할 때, 부분합 Sn을 이용해서 표현. 

무한급수 값은 실수(Nombre réel).

	설명	식
발산	극한이 존재하지 않음.
수렴	변수가 일정한 값에 한없이 가까워지는 것.

위 식을 이용해서, 

 

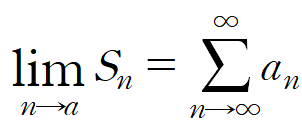
III. 판단법

III-1. 발산 판정 Jugement de divergence

위의 조건에 따라서,

최종 발산판정법

 

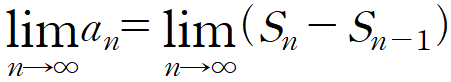
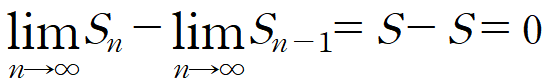
III-2. 비교 판정 Jugement comparaison

급수의 수렴여부를 판정하기위해 변수a와 b를 비교해서 수렴여부를 결정하는 판정법.

정수n에 대해,

 

III-3. 적분 판정 Jugement intégration

급수의 각 항이 양수일때 사용가능. 이상적분*을 활용하여 판정함.

*적분의 극한을 취한 것으로, 무한한 넓이를 다루는 정적분의 한 형태.

 

III-4. 항비 판정

자주 사용되는 판정법으로서, 연속한 항의 비에대한 극한을 판정하는 방법.

수렴여부를 판정하기 위해 초항a, 공비r인 급수에서 [a⒩ > 0일때], 

조건	내용	판정식
r > 1	발산급수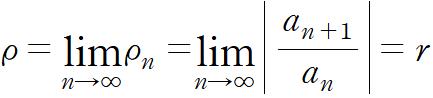
r < 1	수렴급수
r = 1	급수의 수렴여부 결정 불가

 

III-5. 근 판정

실수(Nombre réel)항의 급수 수렴여부를 판정하는 판정법.

조건	내용	판정식
C > 1	발산급수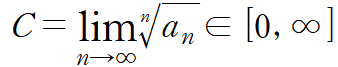
C < 1	수렴급수
C = 1	발산, 수렴 둘다 가능